Balanced Binary Tree

Problem Link

Balanced Binary Tree (opens in a new tab)

Problem Statement

• This is a binary tree problem and NOT a binary search tree problem!!
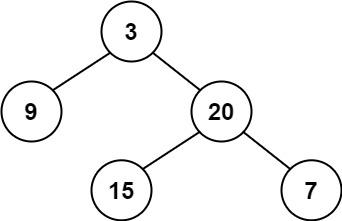
• Here, the heights are balanced because, from every point, the difference in heights of the nodes are less than or equal to 1 ** Eg: height at the root is balanced because: height from the left = 1 (only one node) and height from the right = 2(two nodes): 2-1 = 1
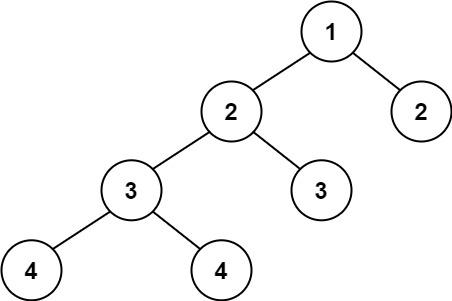
• The heights are not balanced here. Check at the height at the root node. The height of the tree from the left: 3 and from the right: 1 = 2>1
• One more thing to remember is how to find the height of the node:

Math.max(left,right)+1 Balanced Binary Tree: Math.abs(left,right)<1 A null tree is a balanced tree!

Algorithm

We need to go through each level -> DFS

• Base case: if root is null, return true
• To find height of a node, make a function to do so.
• If your height is -1, return false Function for height:
• Base case: root is null? return 0
• find the height of left and right recursively
• if the absolute difference of left and right>-1, return -1
• if either left or right is -1? return -1

Code

class Solution {
    public boolean isBalanced(TreeNode root) {
      if (root==null){
          return true;
      }
      if (height(root)==-1){
          return false;
      }
      return true;
    }
 
    private int height(TreeNode root){
        if (root==null){
            return 0;
        }
        int left = height(root.left);
        int right = height(root.right);
        if (left==-1 || right==-1){
            return -1;
        }
        if (Math.abs(left-right)>1){
            return -1;
        }
 
        return Math.max(left,right)+1;
    }
}